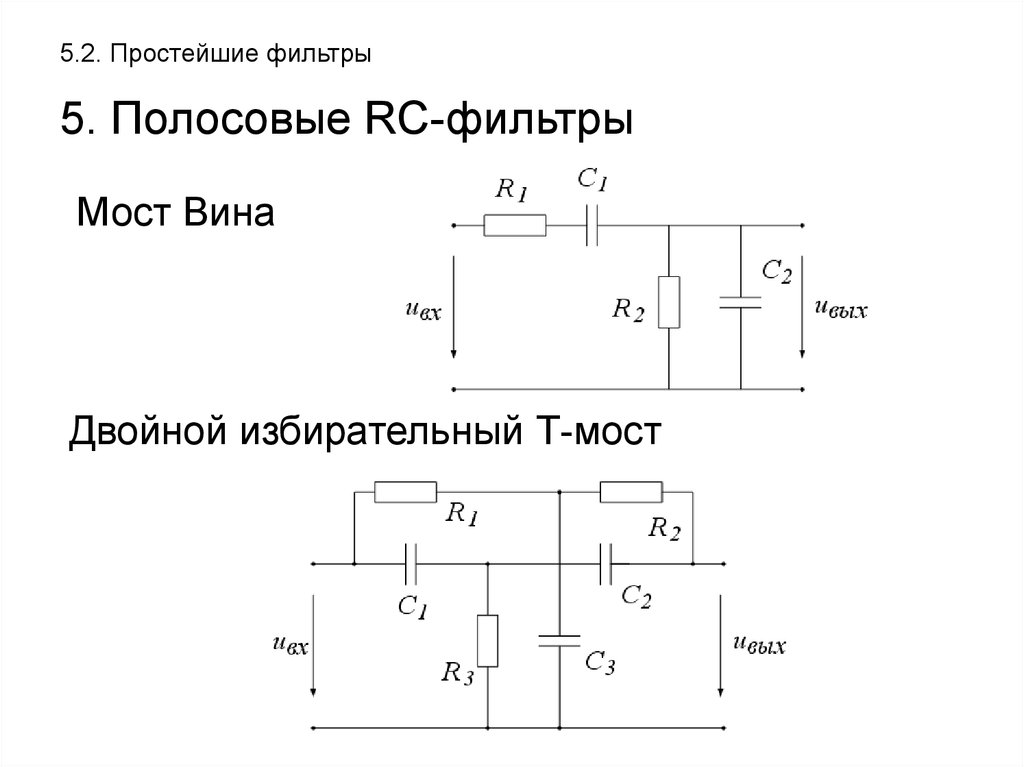
Пассивные полосовые фильтры можно изготовить, соединив вместе фильтр низких частот и фильтр высоких частот.
Полосно-пропускающие фильтры могут использоваться для изоляции или фильтрации определенных частот, которые находятся в определенной полосе или диапазоне частот. Частота среза или точка ƒc в простом пассивном RC-фильтре может точно контролироваться с помощью одного резистора, включенного последовательно с неполяризованным конденсатором, и в зависимости от того, как они подключены, мы видели, что получается либо низкочастотный, либо высокочастотный фильтр.
Одно из простых применений этих типов пассивных фильтров — использование в усилителях звука или схемах, например, в фильтрах кроссовера громкоговорителя или регуляторах тембра предварительного усилителя. Иногда необходимо пропускать только определенный диапазон частот, которые не начинаются с 0 Гц (постоянный ток) или заканчиваются в верхней высокочастотной точке, но находятся в определенном диапазоне или полосе частот, узкой или широкой.
Соединяя или «каскадируя» вместе одну цепь фильтра низких частот с цепью фильтра высоких частот, мы можем получить другой тип пассивного RC-фильтра, который пропускает выбранный диапазон или «полосу» частот, которые могут быть как узкими, так и широкими, при этом ослабляя все те, которые находятся за пределами этого диапазона. Этот новый тип пассивного фильтра создает частотно-избирательный фильтр, известный как Band Pass Filter или сокращенно BPF.
Схема полосового фильтра
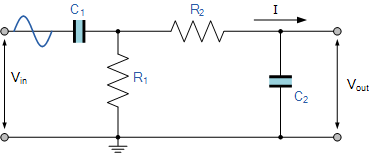
В отличие от фильтра низких частот, пропускающего только сигналы низкого диапазона частот, или фильтра высоких частот, пропускающего сигналы более высокого диапазона частот, полосовые фильтры пропускают сигналы в пределах определенной «полосы» или «разброса» частот, не искажая входной сигнал и не внося дополнительного шума. Эта полоса частот может быть любой ширины и обычно называется полосой пропускания фильтра.
Полоса пропускания обычно определяется как диапазон частот, существующий между двумя заданными точками отсечения частот ( ƒc ), которые на 3 дБ ниже максимального центра или резонансного пика, при одновременном ослаблении или затухании остальных за пределами этих двух точек.
Тогда для широко разнесенных частот мы можем просто определить термин «полоса пропускания», BW, как разницу между точками нижней частоты среза ( ƒcLOWER ) и верхней частоты среза ( ƒcHIGHER ). Другими словами, BW = ƒH — ƒL. Очевидно, что для правильной работы полосового фильтра частота среза фильтра низких частот должна быть выше частоты среза фильтра высоких частот.
«Идеальный» полосовой фильтр пропускания может также использоваться для изоляции или фильтрации определенных частот, лежащих в определенной полосе частот, например, для подавления шума. Полосно-пропускающие фильтры известны как фильтры второго порядка (двухполюсные), потому что в их схеме есть «два» реактивных компонента — конденсаторы. Один конденсатор в цепи низких частот и другой конденсатор в цепи высоких частот.
Частотная характеристика полосового пропускающего фильтра 2-го порядка
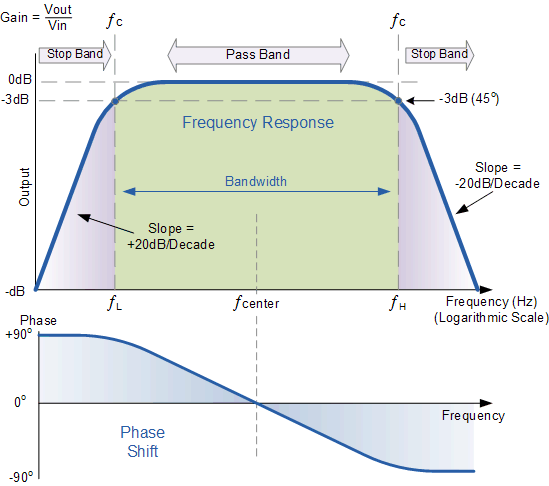
Приведенный выше график Боде или кривая частотной характеристики показывает характеристики полосового фильтра. Здесь сигнал ослабляется на низких частотах, а выходное напряжение увеличивается с наклоном +20 дБ/декада (6 дБ/октава), пока частота не достигнет точки «нижней отсечки» ƒL. На этой частоте выходное напряжение снова составляет 1/√2 = 70,7% от значения входного сигнала или -3 дБ (20*log(VOUT/VIN)) от входного.
Выходной сигнал продолжает усиливаться до достижения точки «верхней отсечки» ƒH, где выходной сигнал уменьшается со скоростью -20 дБ/декада (6 дБ/октава), ослабляя любые высокочастотные сигналы. Точка максимального выходного усиления обычно является средним геометрическим двух значений -3 дБ между нижней и верхней точками отсечки и называется «центральной частотой» или «резонансным пиком» ƒr. Это среднее геометрическое значение рассчитывается как ƒr 2 = ƒ(UPPER) x ƒ(LOWER).
Полосовой фильтр считается фильтром второго порядка (двухполюсным), поскольку в его структуре есть «два» реактивных компонента, то фазовый угол будет в два раза больше, чем у ранее рассмотренных фильтров первого порядка, т.е. 180o. Фазовый угол выходного сигнала опережает входной на +90o до центральной или резонансной частоты, ƒr точки, где он становится «нулем» градусов (0o) или «синфазным», а затем изменяется в сторону отставания от входного на -90o по мере увеличения выходной частоты.
Верхняя и нижняя точки частоты среза для полосового фильтра могут быть найдены по той же формуле, что и для фильтров низких и высоких частот, например.
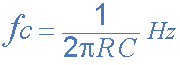
Тогда очевидно, что шириной полосы пропускания фильтра можно управлять с помощью расположения двух точек частоты среза двух фильтров.
Пример полосового фильтра No1
Необходимо построить полосовой фильтр второго порядка с использованием RC-компонентов, который будет пропускать только диапазон частот выше 1 кГц (1 000 Гц) и ниже 30 кГц (30 000 Гц). Предполагая, что оба резистора имеют значения 10kΩ, рассчитайте значения двух необходимых конденсаторов.
Этап фильтра высоких частот
Значение конденсатора C1, необходимое для получения частоты среза ƒL 1 кГц при значении резистора 10 кОм, рассчитывается следующим образом:
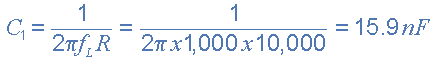
Тогда значения R1 и C1, необходимые для каскада высоких частот, чтобы обеспечить частоту среза 1,0 кГц, следующие: R1 = 10kΩ и, с точностью до предпочтительного значения, C1 = 15nF.
Этап фильтра низких частот
Значение конденсатора C2, необходимое для получения частоты среза ƒH 30 кГц при значении резистора 10 кОм, рассчитывается следующим образом:
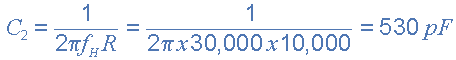
Тогда значения R2 и C2, необходимые для низкочастотного каскада, чтобы обеспечить частоту среза 30 кГц, составляют R = 10 кОм и C = 530 пФ. Однако ближайшим предпочтительным значением рассчитанного значения конденсатора 530пФ является 560пФ, поэтому вместо него используется это значение.
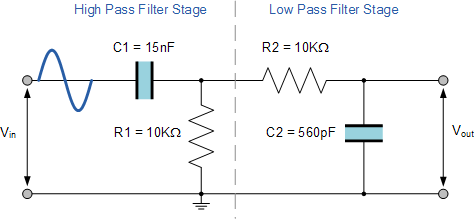
Учитывая, что значения сопротивлений R1 и R2 равны 10kΩ, а значения конденсаторов C1 и C2, найденные для фильтров высоких и низких частот, равны 15nF и 560pF соответственно, схема нашего простого пассивного полосового фильтра имеет вид.
Законченная схема полосового фильтра
Резонансная частота полосового фильтра
Мы также можем рассчитать «резонансную» или «центральную частоту» (ƒr) полосового фильтра, когда выходное усиление достигает максимального или пикового значения. Это пиковое значение не является средним арифметическим верхней и нижней точек отсечки -3 дБ, как можно было бы ожидать, а представляет собой «геометрическое» или среднее значение. Это среднее геометрическое значение рассчитывается, например, как ƒr 2 = ƒc(UPPER) x ƒc(LOWER):
Уравнение центральной частоты
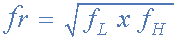
Где, ƒr — резонансная или центральная частота
ƒL — нижняя точка частоты среза по уровню -3 дБ
ƒH — верхняя точка среза частоты -3 дБ
и в нашем простом примере выше, рассчитанные частоты среза составили ƒL = 1 060 Гц и ƒH = 28 420 Гц, используя значения фильтра.
Подставив эти значения в вышеприведенное уравнение, можно получить центральную резонансную частоту:

Краткое описание полосового фильтра
Простой пассивный полосовой фильтр может быть изготовлен путем каскадного соединения одного фильтра низких частот с фильтром высоких частот. Диапазон частот в герцах между нижней и верхней точками среза по уровню -3 дБ комбинации RC называется «полосой пропускания» фильтра.
Ширина или частотный диапазон полосы пропускания фильтра может быть очень маленькой и селективной или очень широкой и неселективной в зависимости от используемых значений R и C.
Точка центральной или резонансной частоты является средним геометрическим нижнего и верхнего срезов. На этой центральной частоте выходной сигнал максимален, а фазовый сдвиг выходного сигнала такой же, как и входного.
Амплитуда выходного сигнала полосового фильтра или любого другого пассивного RC-фильтра всегда будет меньше амплитуды входного сигнала. Другими словами, пассивный фильтр также является аттенюатором, дающим коэффициент усиления по напряжению менее 1 (Единство). Чтобы обеспечить выходной сигнал с коэффициентом усиления по напряжению больше единицы, в конструкции схемы требуется некоторая форма усиления.
Пассивный полосовой фильтр классифицируется как фильтр второго порядка, поскольку в его конструкции есть два реактивных компонента — конденсаторы. Он состоит из двух отдельных фильтрующих RC-цепей, которые сами являются фильтрами первого порядка.
При каскадном соединении нескольких фильтров результирующая схема будет называться фильтром «n-го порядка», где «n» означает количество отдельных реактивных компонентов и, следовательно, полюсов в цепи фильтра. Например, фильтры могут быть 2-го порядка, 4-го порядка, 10-го порядка и т.д.
Чем выше порядок фильтра, тем круче будет наклон при n раз -20 дБ/декада. Однако один конденсатор, полученный путем объединения двух или более отдельных конденсаторов, все равно остается одним конденсатором.
Наш пример выше показывает кривую выходной частотной характеристики для «идеального» полосового фильтра с постоянным коэффициентом усиления в полосе пропускания и нулевым коэффициентом усиления в полосе останова. На практике частотная характеристика этой схемы полосового фильтра не будет такой же, поскольку входное реактивное сопротивление цепи высоких частот будет влиять на частотную характеристику цепи низких частот (компоненты подключены последовательно или параллельно) и наоборот. Один из способов преодоления этой проблемы — обеспечить электрическую развязку между двумя цепями фильтра, как показано ниже.
Буферизация отдельных ступеней фильтра
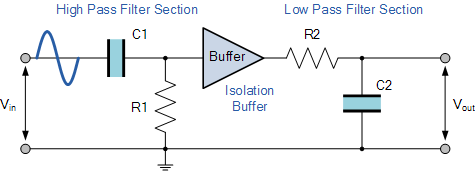
Одним из способов объединения усиления и фильтрации в одной схеме является использование операционного усилителя (Op-amp), примеры которого приведены в разделе «Операционный усилитель». В следующем уроке мы рассмотрим схемы фильтров, в которых операционный усилитель используется не только для усиления, но и для обеспечения изоляции между каскадами. Такие схемы фильтров обычно называются активными фильтрами.